
위 논문은 CNN, LSTM, GRU 등의 모델을 이용하여 CAN Sensor의 시계열 데이터의 이상 상황을 탐지를 한다는 연구입니다.
Abstract
CAN 센서에서 생성된 시계열 데이터를 분석하여 비지도 학습을 기반으로 한 Anomaly Detection을 제안합니다.
작은 규모의 RNN과 CNN을 사용하여 다차원적인 시계열 데이터를 효율적으로 처리하고자 합니다.
Introduction and Related Work
자동차 산업에서 Predictive Maintenance는 차량에서 발생하는 이상과 고장을 사전에 감지하는 것을 목표로 합니다.
차량은 복잡하고 다양한 센서들의 데이터로 구성되어 Multidimensional Time Series Data가 생성되게 됩니다.
Car Time Series Extracted from the CAN Bus
The Data and the Car

- ECU : 자동차의 다양한 기능을 제어하는 전자 제어 장치로서, 센서로부터 데이터를 수집하고 액추에이터 제어
- CAN Bus : ECU 간의 통신을 담당하는 네트워크 입니다. CAN 버스를 통해 주고받는 메시지에는 차량의 상태와 작동 정보를 포함한 다양한 데이터가 포함됩니다.
- spy box : CAN 버스에서 데이터를 모니터링하고 수집하는 장치이며, CAN 버스를 통해 전달되는 모든 메시지를 캡처하여 클라우드 데이터베이스로 전송합니다
- Cloud Database : Spy Box에서 수집된 CAN 버스 데이터를 저장하는 클라우드 기반 데이터베이스입니다.
- Resampling : Cloud DB에 저장된 CAN 데이터는 불규칙한 간격으로 수집될 수 있기 때문에, 일정한 시간 간격으로 다시 Resampling됩니다.
- Predictor :Resampling된 데이터는 예측 모델에 입력됩니다.
- Anomaly Detector : 예측 데이터와 실제 데이터를 비교하여 이상치를 탐지합니다.
Our Dataset
차량의 주행 테스트에서 수집된 486개의 변수를 포함하고 있으며, 4개월동안 수집되었고 총 17GB의 데이터가 수집되었음. 데이터는 10Hz 속도로 샘플링되었고, 변수의 복잡성을 고려해 85개의 주요 변수만 남기고 나머지는 필터링 되었음. 최종적으로 1Hz로 Resamping되어 사용하였습니다.
Labels
오일 압력과 관련된 이상 현상이 감지된 3683개의 타임스탬프로 구성됩니다.
이상 현상으로는 오일 압력, 오일 온도, 평균 유효 토크, RPM, 엔진 냉각수 온도 등이 있지만 여기서는 오일 압력 행동을 이상으로 정의하였음.
System Model and Problem Formulation
System Model

n개의 샘플로 구성된 시계열 T를 고려했으며, 각 샘플은 변수를 나타내는 m차원의 인덱스 벡터입니다.
각 시계열 xt는 예측 모델을 통해 예측된 값 ^xt+1와 비교되어 예측 오차 et+1를 계산하고, 이를 통해 이상 여부를 판별합니다.
이상 레이블은 ^at로 표현되며, 이진값으로 0-정상 or 1-비정상 값을 가집니다.
Unsupervised Anomaly Detection
LSTM기반 모델을 사용하여 예측 오류를 기반으로 한 이상 탐지 방법을 제시

50개의 cell과 2개의 Layer를 가진 LSTM을 semi-supervised threshold optimization을 사용하였고,
100 epochs, learning_rate : 10−3, window = 100을 사용하였습니다.
평균적으로 위 논문에서 사용한 LSTM이 평균적으로 가장 높은 성능을 보였습니다.
LSTM Predictor
Anomaly Detector의 첫번째 block은 LSTM은 신경망으로 구성됩니다.
LSTM Cell은 아래의 그림으로 설명됩니다. 각 셀은 반복적으로 작동하며 벡터 ct와 ht를 출력합니다.

사용된 스택된 LSTM은 두 개의 레이어로 구성되어 있으며, 입력 샘플을 받아서 다음 샘플을 예측합니다.
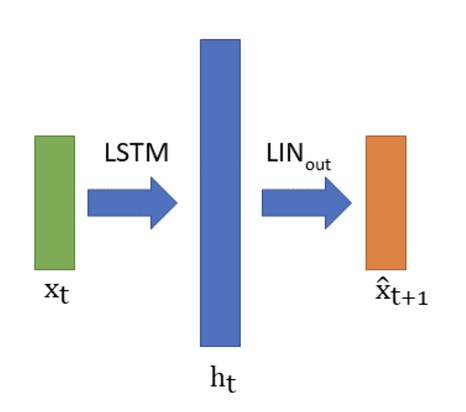
위 그림과 같이 벡터 ht를 xt+1의 예측 값으로 변환합니다.
CNN Predictor
CNN의 한계는 convolutional window보다 긴 시간적인 정보를 통합할 수 없다는 것입니다.
⇒ Time window의 크기가 10이라면, 10까지의 연속된 데이터 포인트만 처리할 수 있음. 그 범위를 벗어나는 긴 시간적 패턴은 직접적으로 포착할 수 없음.
예를 들어, 몇달치 데이터를 반영하고 싶은데 CNN의 윈도우 크기가 10이라면 10일치 데이터만을 사용하여 예측을 수행함. 그럼 늘리면되잖아? ⇒ 계산양 너무 많아져
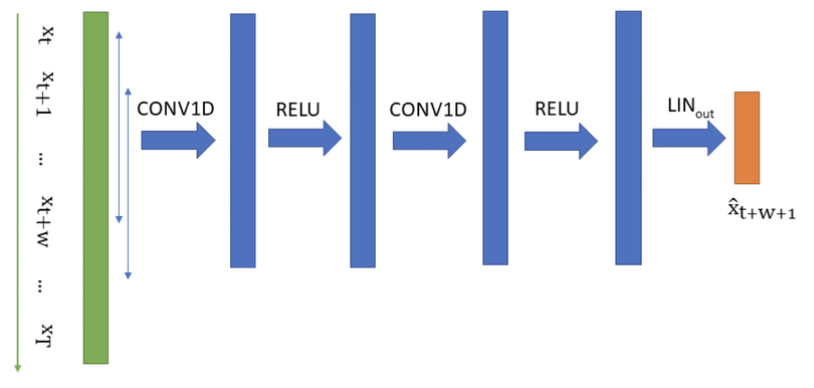
- 만약에 window가 5라면, 첫번째 윈도우는 {x1,x2,x3,x4,x5}일 것이고, 두번째 윈도우는 {x2,x3,x4,x5,x6}가 되겠죠?
- 그래서 총 n개의 데이터라고 한다면, n10개의 구간이 생기는 것입니다!
무튼 이렇게 해서 {xt,...,xt+w}를 기반으로 다음 시계열 ^xt+w+1을 예측할 수 있습니다.
GRU Predictor
GRU는 각 셀에 더 적은 수의 게이트를 포함하여 더 가벼운 RNN을 형성하는 LSTM의 간소화된 버전입니다. 구조는 LSTM과 동일한 구조입니다.
간소화되었어도 더 적은 매개변수로도 LSTM과 동일하거나 더 나은 성능을 발휘하 수도 있습니다.
Performance
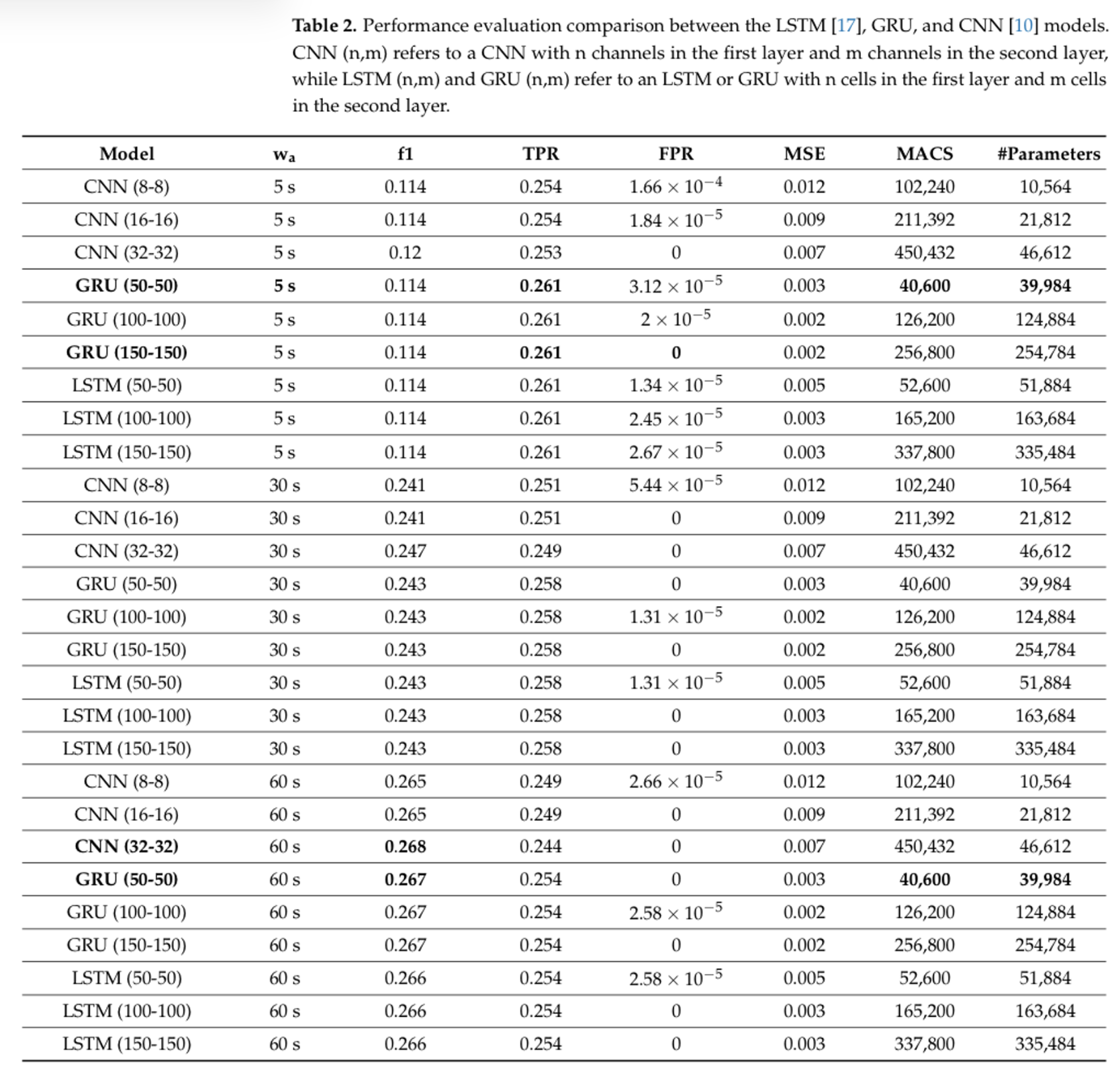
- wa : 윈도우 크기
- f1 : F1 스코어, 정밀도와 재현율의 조화 평균
- TPR : True Positive Rate
- FPR : False Positive Rate
- MSE : Mean Squared Error
- MACS : Multiply-Accumulate Operations per Second
- #Parameters : 모델의 총 매개변수 수
결론 :
- 윈도우 크기가 클수록 모델의 성능이 향상되었음
- GRU와 LSTM 모델은 비교적 적은 매개변수로도 높은 성능을 발휘할 수 있으며, 특히 GRU 모델이 좋은 성능을 보임
- CNN 모델은 윈도우 크기 60일 때 가장 높은 F1 점수를 기록하지만, 당연하게도 매개변수와 계산량이 많다는 문제가 있음
Anomaly Detecion
훈련 중에 각 샘플 xt에 대해 predictor가 ^xt+1를 출력합니다. 그런 다음, 예측값과 실제 샘플 간의 모든 차원과 시간에 대한 MSE를 계산합니다.
MSE=1nmn−1∑t=0||(^xt−xt)2||1
||∗||1는 Norm 1을 의미합니다.
이 오류는 Gradient Descent 최적화를 사용하여 predictor를 최적화하기 위한 Loss Function으로 사용되었습니다. 위 방법과 LSTM or GRU를 사용하여 다양한 길이의 시계열 데이터를 최대한 활용할 수 있었습니다.
시간 의존성을 해결하기 때문에 데이터가 다양한 길이라도 학습할 수 있기 때문 → 데이터 길이가 일관되지 않을 때 특히 유용.
대부분의 변수가 상관되어 있다고 가정하고 모든 m 변수를 predictior에 제공하여 더 복잡한 시간적 및 상관관계를 포착하고 신호를 더 잘 예측할 수 있게 하였음.
예측 제곱 오차 : et=(^xt−xt)2
예측 제곱 오차 시계열 : E={e0,e1,...,en−1}
위를 구한 다음, 시계열 E에 이상 확률 방법을 적용하여 이상 점수 st와 Label ^at를 얻었음.
먼저, E의 w 샘플에 대한 슬라이딩 정규 분포의 매개변수 μt와 σ2t를 계산하였음.
μt=∑W−1i=0et−iW
σ2t=∑W−1i=0(et−i−μt)2W−1
그런 다음, Gaiussian tail 확률 Q-function을 사용하여 anomaly score를 얻었습니다.
st=1−Q(~μt−μtσt)
~μt=∑W′−1i=0et−iW′
마지막으로, 임계값 벡터 θ를 사용하여 발견된 이상을 계산했습니다.
^ati={1,if sit≥θi0,otherwise
각 변수는 고유의 매개변수를 사용하여 개별적으로 처리되었기 때문에 병렬적으로 처리된 m 개의 이상 가능성이 있습니다.
마지막으로 최소한 하나의 변수가 비정상으로 판정된 타임스탬프 AT를 정의하였습니다.
AT={t∈[t0,tn−1] | ||^at||1>0}
위 식은 타임스탬프 t가 이 범위동안 하나 이상의 변수에 대해 이상이 감지되었음을 의미하는 집합임.
Results
- Epochs : 300
- Learning Rate : 10−4
- Optimizer : Adam
- Subsequences : 데이터를 100 Point씩 나누어 2000개의 하위 시퀀스로 학습 시킴
Evaluation with Labels
Label은 오일 압력 이상으로 정의했으며, 이 이상 행동은 instantaneous 하지않고 몇초동안 나타납니다. 그러므로 time window Wa를 고려해야 함.
TP={t∈AT|∃tl∈L,tl−Wa≤t≤tl+Wa}
- t∈AT : 타임스탬프 t가 알고리즘이 이상으로 감지한 타임스탬프 집합 AT에 속함.
- L : 라벨이 있는 타임스탬프의 집합. 즉, 실제로 이상이 발생
FP={t∈AT|∄tl∈L,tl−Wa≤t≤tl+Wa}
TN={t∈[t0,tn−1]∖AT∣∄tl∈L, tl−wa≤t≤tl+wa}
FN={t∈[t0,tn−1]∖AT∣∃tl∈L, tl−wa≤t≤tl+wa}
TPR=|TP|L , FPR=|FP|n , TNR=|TN|n , FNR=|FN|n
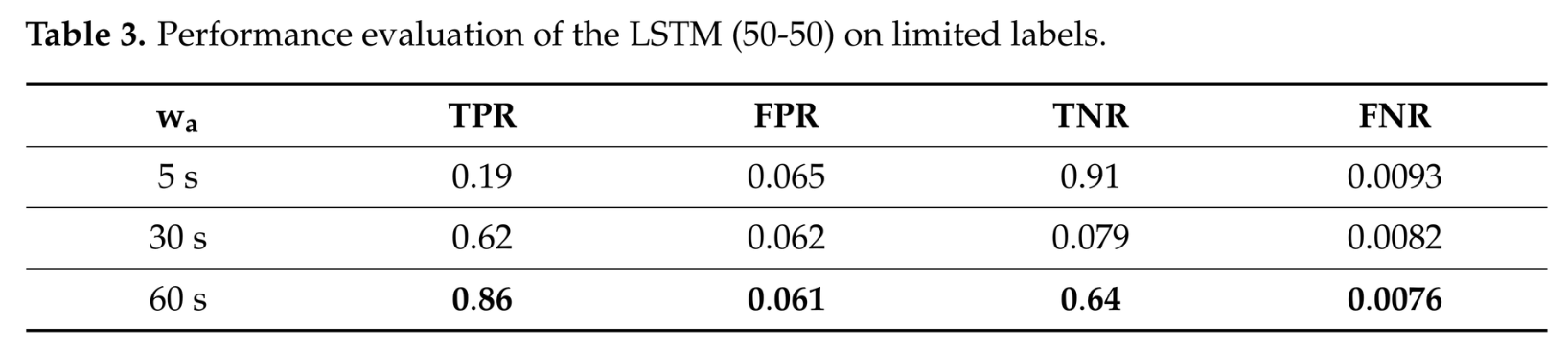
time window를 크게 설정할수록 TPR이 증가하고 FNR이 감소함을 알 수 있습니다.
60초의 time window를 설정했을 때 86%라는 탐지를 달성하였습니다.
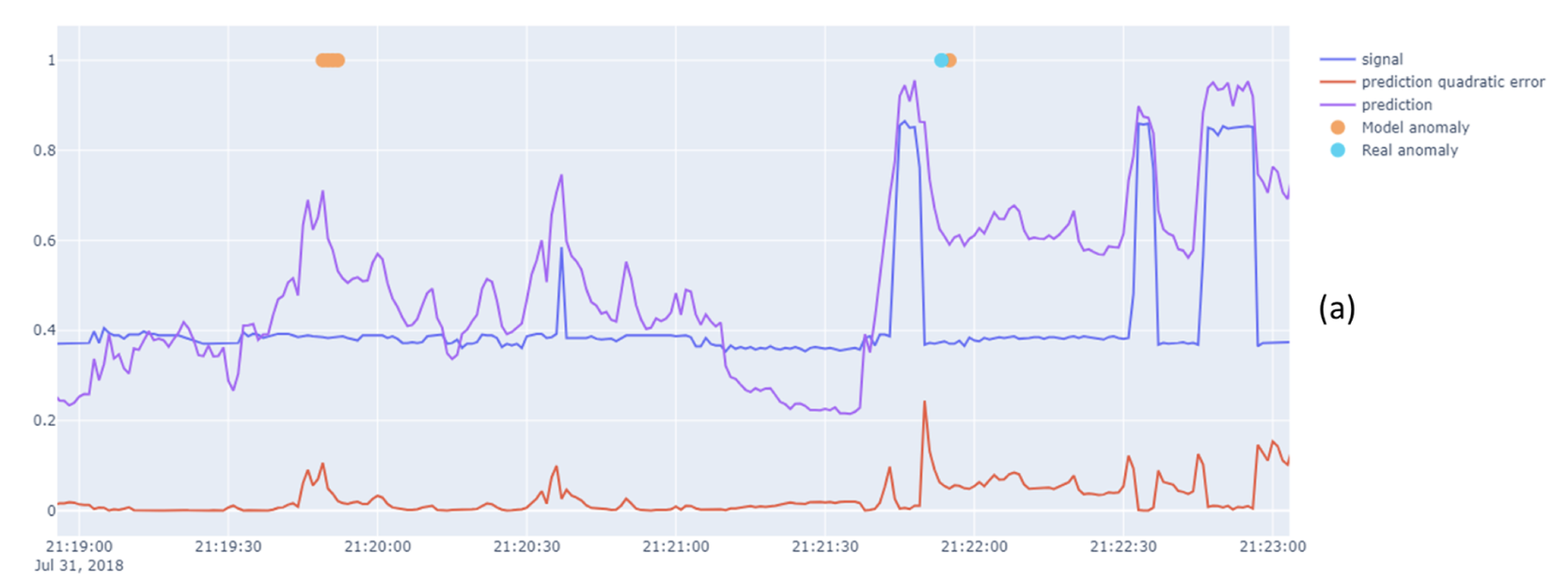
engine oil pressure time series에 대한 그림입니다.
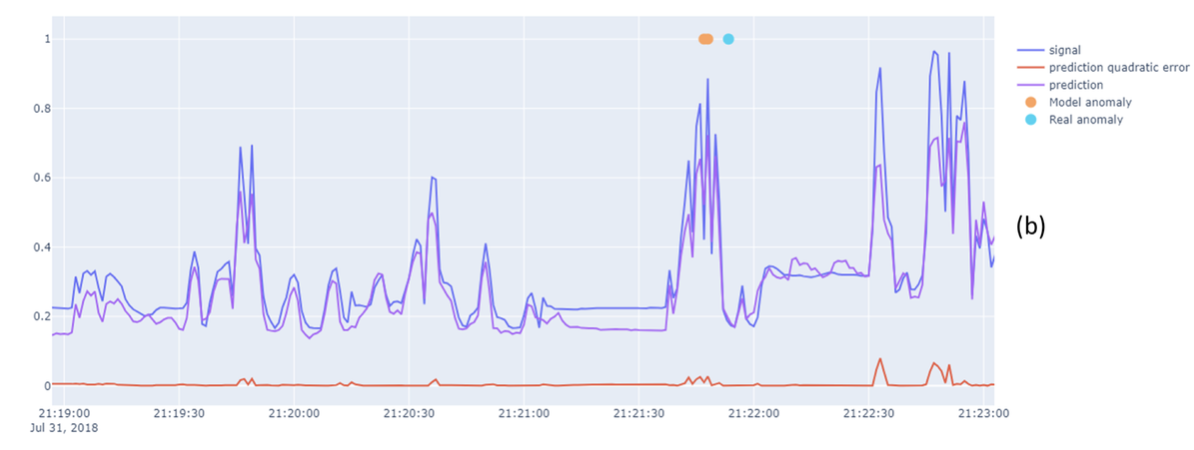
엔진 평균 유효 토크 시계열 데이터에 대한 이상탐지 입니다.
LSTM Computations Costs Comparison

cell 10의 LSTM이 가장 높은 TPR을 보여주지만, FPR도 고려해야 함.
이상 탐지 결과를 평가할 때 고려해야 할 두 가지 요소는 TPR과 FPR입니다.
FPR은 낮을수록, TPR은 높을수록 좋습니다.
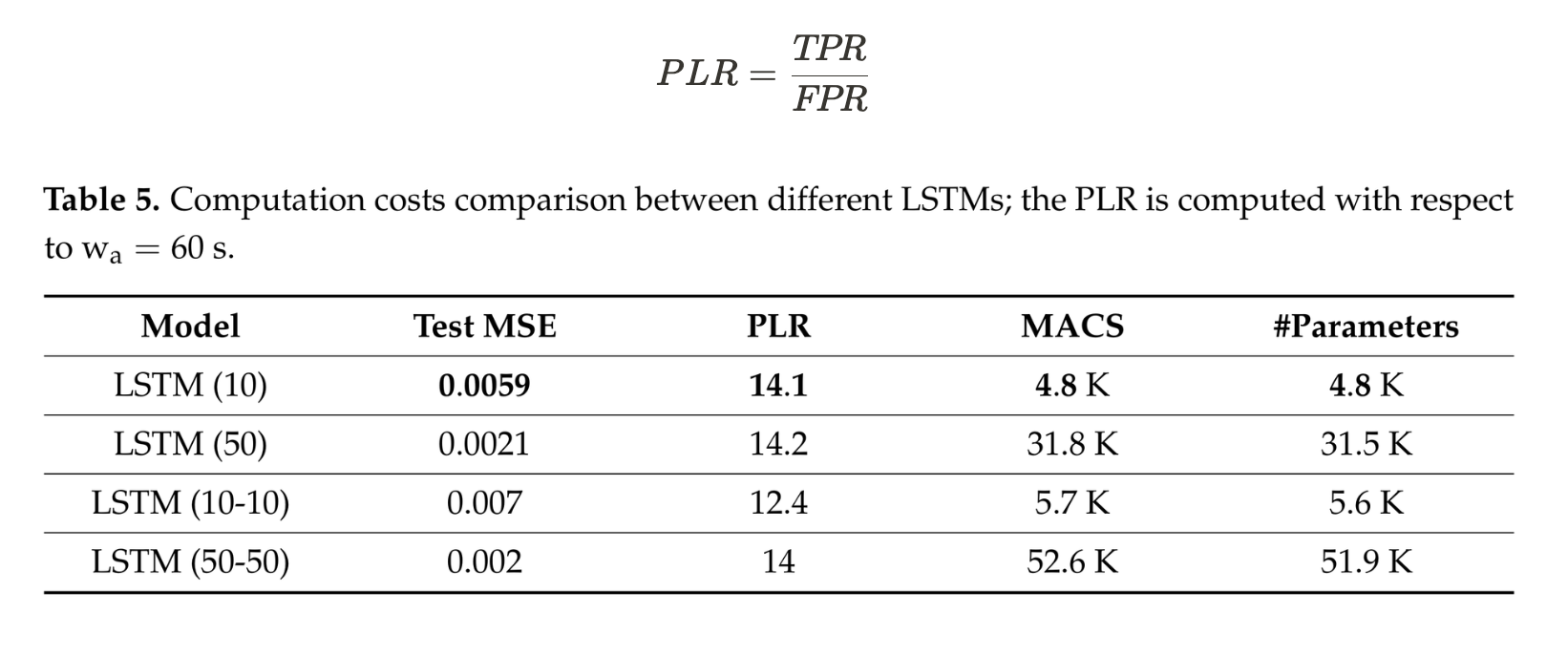
LSTM-50이 14.2로 가장 높은 PLR입니다. LSTM-10도 유사하며, 계산 비용-MACS이 LSTM-50보다 훨씬 낮으므로 임베디드 시스템에 더 적합하다고 판단됩니다.
CNN Model도 평가하고자 하였으며, recall과 precision으로 평가하였습니다.
recall=TPP , precision=TPPP , f1=2precision∗recallprecision+recall
가장 높은 f1-score는 CNN:32-32이 기로했으며, GRU 또한 좋았습니다.
Discussion and Future Works
특정 이상 행동-오일압력만을 표현하기에 모델을 완전히 평가하긴 어렵기에 더 많은 변수를 사용하여 평가하지 못한게 한계
'Papers > Anomaly Detection' 카테고리의 다른 글
| [논문리뷰] Change Point Enhanced Anomaly Detection for IoT Time Series Data 0 | 2024.08.02 |
|---|
